Implement an AVL Tree with Go

9 min readAug 25, 2022

What is AVL tree?

In computer science, an AVL tree (named after inventors Adelson-Velsky and Landis) is a self-balancing binary search tree. It was the first such data structure to be invented. In an AVL tree, the heights of the two child subtrees of any node differ by at most one.
— wikipedia

There is a big disadvantage in naïve binary search trees. For example, if we insert nodes in increasing order, the binary tree will become just a linked list. That is to say, the time complexity of the search will become O(n), where n is the number of all nodes.

AVL is a self-balancing binary search tree. It is guaranteed that the time complexity of searching for nodes is always O(log n), regardless of the order in which you insert the nodes.

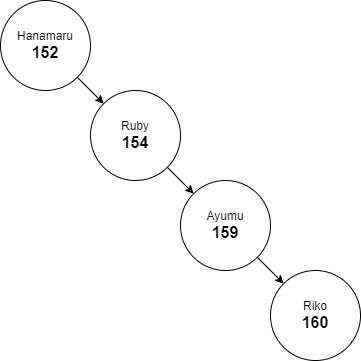
Figure1. If we insert nodes in increasing order.

Definition

AVL tree checks the height of the left and the right sub-trees and assures that the difference is not more than 1. That is, AVL trees make sure that |height(node.left)-height(node.right)| ≤ 1

How to calculate the height of nodes?

height(null) = -1
height(node) = max(Height(Node.left), height(node.right)) + 1

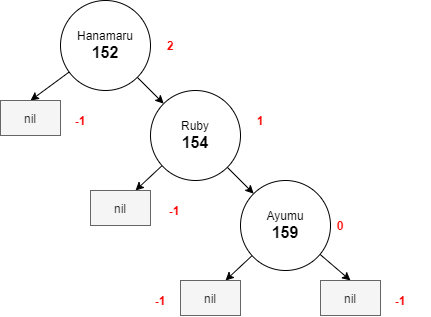
Figure 2. An example of calculating the height of nodes. The binary tree is not an AVL tree.

Figure 3. Another example of calculating the height of nodes. The binary tree is an AVL tree.

In Figure 2, The height of the left subtree of hanamaru is -1, and the height of the right subtree hanamaru is 1. Because 1-(-1) > 1, this binary tree is not an AVL tree. As for Figure 3, there are no nodes that betray the rules of AVL trees, thus this tree is an AVL tree.

Rotation

To modify a binary tree to an AVL tree, we can use rotation. To realize what is rotation, first, please see the 4 states below.

Figure 4. Four states that we should consider. (a) RR type (b) LL type © RL type (d) LR type

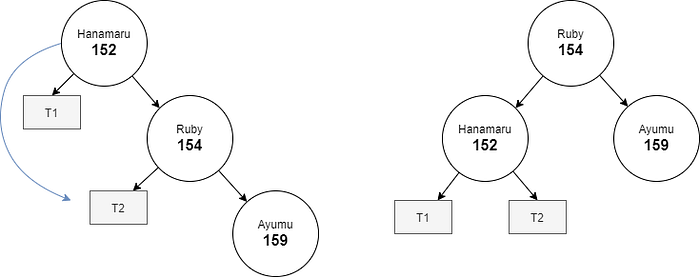
All of the above 4 states can be converted to an AVL tree. We can use left rotation to convert Figure 4(a) into an AVL tree.

Figure 5(a). An example of left rotation for an RR-type tree.

We can use the right rotation to convert Figure 4(b) into an AVL tree.

Figure 5(b). An example of right rotation for an LL-type tree.

However, how do rotate RL type and LR type in Figure 4(c) and Figure 4(d) respectively? We can rotate them twice!

For RL types, right rotate Ayumu to convert it to RR type.

Figure 5(c). An example of rotation an RL-type tree in order to convert it to RR type.

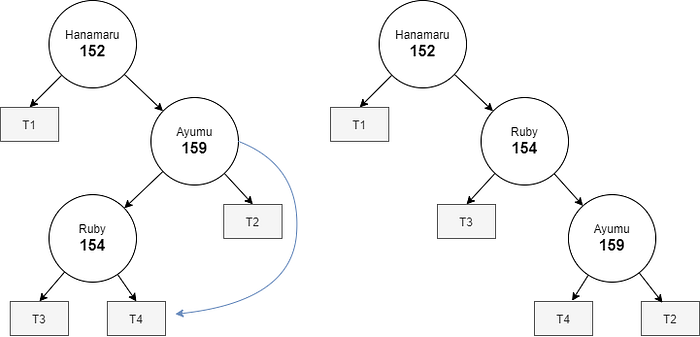
Hanamaru.rihgt.rightRotate()
Hanamaru.leftRotate()

As for LR types, left rotate Hanamaru to convert it to LL type.

Figure 5(d). An example of rotation an LR-type tree in order to convert it to LL type.

Ayumu.left.leftRotate()
Ayumu.rightRotate()

Implement

AVLNode

Begin implementing the AVL tree, we create a structure for its nodes.

The tree node not only needs the left node and the right node but also needs the height value.

Then, we should define how to update the height value.

// pseudo code
if node has no child {
    height = 0
}else{
    height = max(node.left.height, node.right.height)+1
}

updateHeight() updates the height value in the node n . When calling updateHeight(), we should make sure that all the children of node n have the correct height.

Next, we need to specify how to rebalance the tree. We can build a function that rotates the subtree by given the root of the subtree and returning the new node of the subtree. For example, see Figure 5(a), after calling hanamaru.LeftRotation(), the left rotation method should return new root, i.e., ruby.

rightRotation() and leftRotation() rotates the subtree whose root is n and returns the root node of the new subtree.

It is not easy to understand how they work. So, I draw a graph to interpret it.

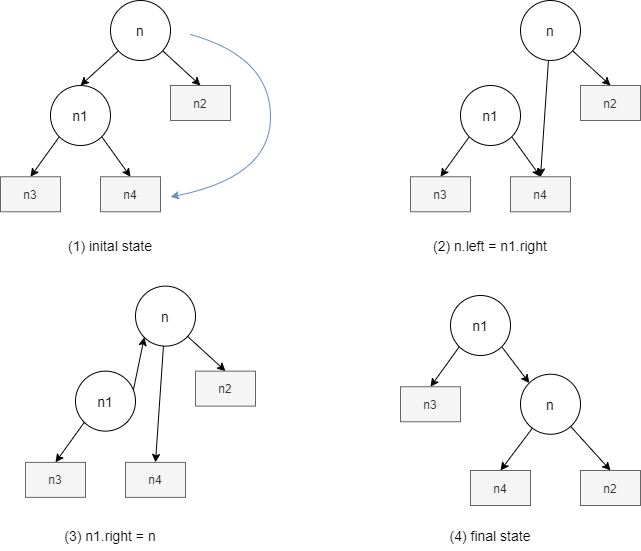
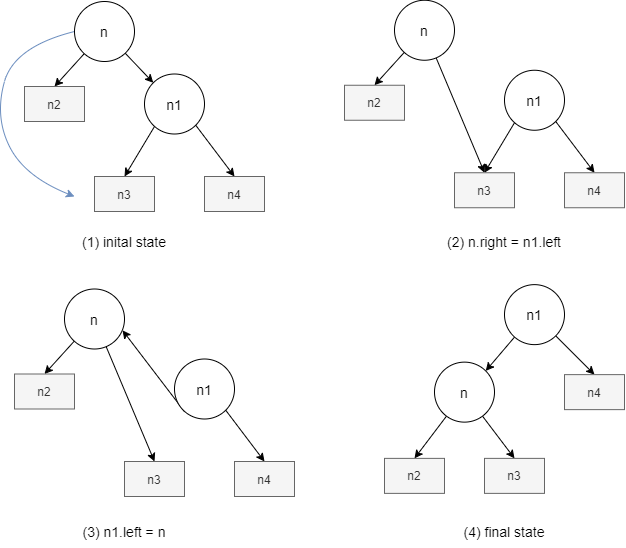
Figure 6(a). The steps of right rotation

In Figures 6(a) and 6(b), we can observe that the rectangle node’s children, n2, n3, and n4, do not be changed, so we do not need to update the height of the rectangle nodes. As for the circle nodes, n and n1, whose children were changed after rotating. Thus, we need to update the height of n and n1, because n1’s height is dependent on n’s height, we update n’s height first.

After defining the rotation method, we should build a rebalance method that detects the subtree type, and then rotates the subtree to make it satisfy the conditions of the AVL tree.

blanceFactor() calculates the balance factor of the tree node n .
rebalance() reblances the subtree whose root node is n by right rotation or left rotation. It returns the root node of the new balanced subtree.

When the balance factor is 0, 1, or -1, it means the difference between the height of the left subtree and the height of the right subtree are not exceed 1, so we can return the original node directly. However, when the balance factor is bigger than 1, it means that the left subtree is higher than the right subtree. That is, One of two scenarios (LL or LR) could occur. If a given node has a left node and its left node’s balance factor is smaller than zero, then we are faced with the LR-type problem. LR-type or RL-type should be rotated twice.

In this article, I only introduce how to insert a new node and search for a node. I will introduce how to remove nodes in the next article.

So, how to insert a new node into the AVL tree? There are usually 2 methods to insert a new node into the binary search tree. One of them is recursive, and the other one is iterative. When inserting a new node, we should record the nodes that pass through the path in order to recalculate the height of nodes and rebalance the nodes that we passed through.

If we use the iterative method to implement insert(), we should implicitly use a stack to record the path. Or, we can change the structure of AVLNode — adding a new field to record the parent of this node.

type AVLNode struct{
    Key    int
    Val    interface{}
    left   *AVLNode
    right  *AVLnode
    parent *AVLnODE
    height int
}

These methods are more difficult to implement and the performance is not necessarily better. Therefore, we can use the recursive method.

insert() inserts the node m into the subtree whose root node is n and returns the root node of the new subtree.

The search function of the AVL tree is as same as the classic binary search tree.

search() searches the tree whose root node is n and returns a non-nil node if found. If not found the key, returns nil.

AVLTree

Test

To traverse the tree, we still need to implement a traverse function.

Create a test file e.g., avl_test.go .

import (
    "fmt"
    "hash/fnv"
    "testing"
)

func hash(s string) int {
    h := fnv.New32a()
    h.Write([]byte(s))
    return int(h.Sum32() % 255)
}

// go test -run TestAVLTree -v
func TestAVLTree(t *testing.T) {
    tree := new(AVLTree)
    list := []string{
        "Chika", "You", "Ruby",
        "Riko", "Yoshiko", "Mari",
        "Kanan", "Dia", "Hanamaru",
    }

    for _, v := range list {
        fmt.Printf("Insert (%d %s)\n", hash(v), v)
        tree.Insert(NewAVLNode(int(hash(v)), v))
        tree.Do(func(a *AVLNode) {
            l := "nil"
            if left := a.left; left != nil {
                l = fmt.Sprintf("%3d", left.Key)
            }
            r := "nil"
            if right := a.right; right != nil {
                r = fmt.Sprintf("%3d", right.Key)
            }
            fmt.Printf("%3d left: %s right: %s balance: %2d height: %2d\n", a.Key, l, r, a.balanceFactor(), a.height)
        })
        fmt.Println("------------------")
    }
    
    tree.Do(func(a *AVLNode) {
        fmt.Printf("(%d, %s) -> ", a.Key, a.Val)
    })
    fmt.Println()
}

Result:

Insert (60 Chika)  
 60 left: nil right: nil balance:  0 height:  0 
------------------ 
Insert (129 You)
 60 left: nil right: 129 balance: -1 height:  1 
129 left: nil right: nil balance:  0 height:  0 
------------------ 
Insert (7 Ruby) 
  7 left: nil right: nil balance:  0 height:  0
 60 left:   7 right: 129 balance:  0 height:  1 
129 left: nil right: nil balance:  0 height:  0 
------------------ 
Insert (240 Riko) 
  7 left: nil right: nil balance:  0 height:  0 
 60 left:   7 right: 129 balance: -1 height:  2
129 left: nil right: 240 balance: -1 height:  1 
240 left: nil right: nil balance:  0 height:  0 
------------------ 
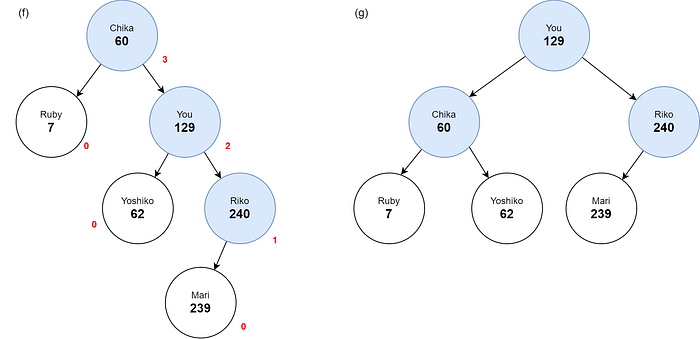
Insert (62 Yoshiko) 
  7 left: nil right: nil balance:  0 height:  0 
 60 left:   7 right: 129 balance: -1 height:  2 
 62 left: nil right: nil balance:  0 height:  0
129 left:  62 right: 240 balance:  0 height:  1
240 left: nil right: nil balance:  0 height:  0 
------------------ 
Insert (239 Mari) 
  7 left: nil right: nil balance:  0 height:  0 
 60 left:   7 right:  62 balance:  0 height:  1 
 62 left: nil right: nil balance:  0 height:  0 
129 left:  60 right: 240 balance:  0 height:  2 
239 left: nil right: nil balance:  0 height:  0 
240 left: 239 right: nil balance:  1 height:  1 
------------------ 
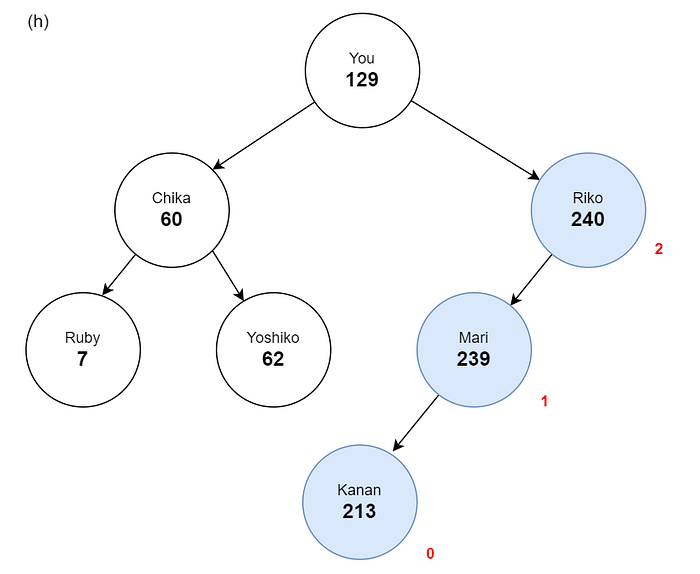
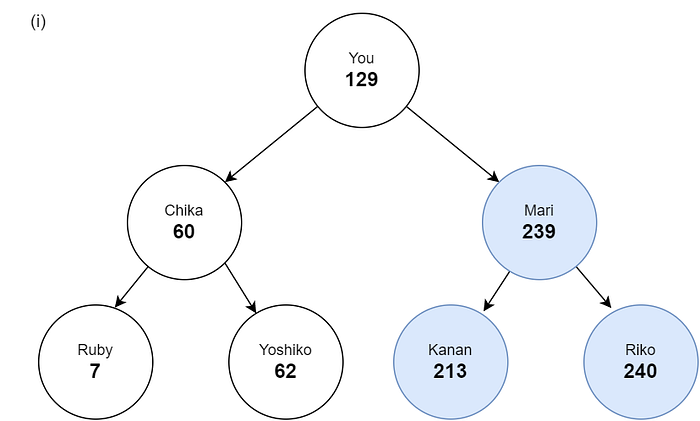
Insert (213 Kanan) 
  7 left: nil right: nil balance:  0 height:  0 
 60 left:   7 right:  62 balance:  0 height:  1
 62 left: nil right: nil balance:  0 height:  0 
129 left:  60 right: 239 balance:  0 height:  2 
213 left: nil right: nil balance:  0 height:  0 
239 left: 213 right: 240 balance:  0 height:  1 
240 left: nil right: nil balance:  0 height:  0 
------------------ 
Insert (152 Dia)   
  7 left: nil right: nil balance:  0 height:  0 
 60 left:   7 right:  62 balance:  0 height:  1
 62 left: nil right: nil balance:  0 height:  0
129 left:  60 right: 239 balance: -1 height:  3
152 left: nil right: nil balance:  0 height:  0 
213 left: 152 right: nil balance:  1 height:  1 
239 left: 213 right: 240 balance:  1 height:  2 
240 left: nil right: nil balance:  0 height:  0
------------------ 
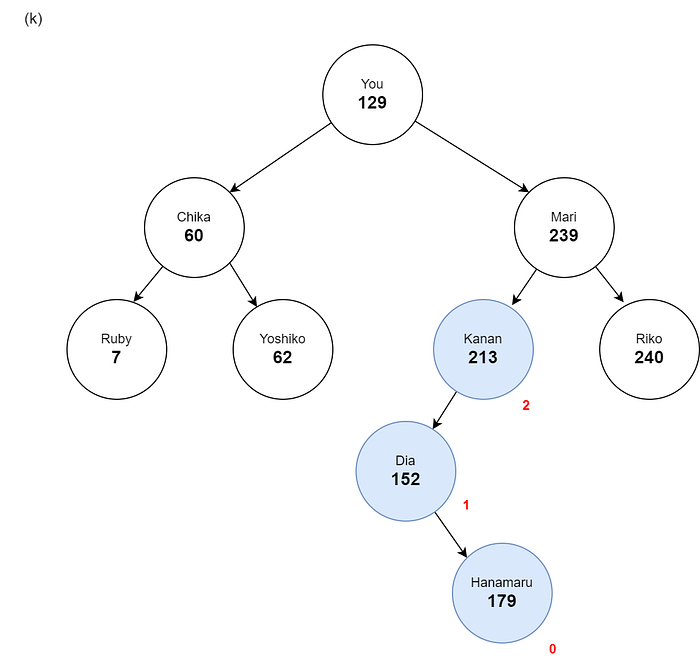
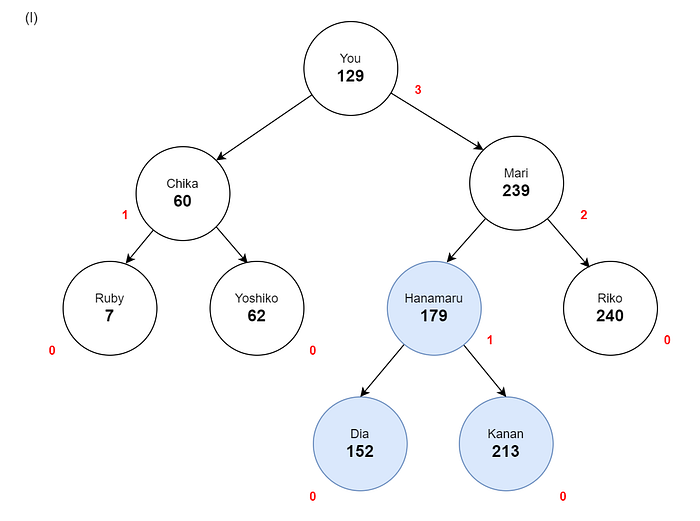
Insert (179 Hanamaru) 
  7 left: nil right: nil balance:  0 height:  0 
 60 left:   7 right:  62 balance:  0 height:  1 
 62 left: nil right: nil balance:  0 height:  0 
129 left:  60 right: 239 balance: -1 height:  3 
152 left: nil right: nil balance:  0 height:  0 
179 left: 152 right: 213 balance:  0 height:  1 
213 left: nil right: nil balance:  0 height:  0 
239 left: 179 right: 240 balance:  1 height:  2
240 left: nil right: nil balance:  0 height:  0
------------------ 
(7, Ruby) -> (60, Chika) -> (62, Yoshiko) -> (129, You) -> (152, Dia) -> (179, Hanamaru) -> (213, Kanan) -> (239, Mari) -> (240, Riko) ->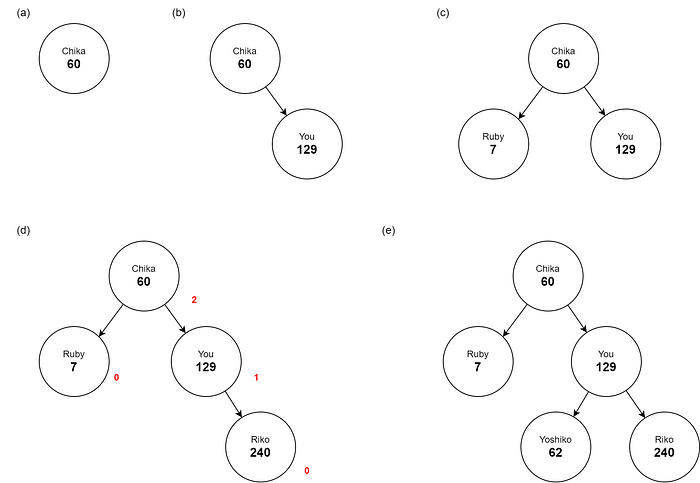

Figure 7(a)~(e). **(a)** Add (60, Chika) **(b)** Add (You, 129) (c) Add (Ruby, 7) **(d)** Add (Riko, 240) **(e)** Add (Yoshiko, 62)

Figure 7(f)~(g). **(f)** Add (Mari, 239) **(g)** After rebalancing

Delete

It is too complex to introduce both deletion and insertion in the same article. Therefore, I will explain how to delete a node in an AVL tree in another article.

Implement an AVL Tree with Go (Part II) | by Kashiwa | Sep, 2023 | Medium

See full code here: https://github.com/ksw2000/Medium/tree/main/implement-an-avl-tree-with-go

See the relative articles: